dexed FM 音作り
アルゴリズム
FM音源はサイン波を出力するオシレータを掛け合わせて音を作る。 DEXEDには、6個のオシレータの組み合わせが32通り用意されている。これをヤマハDX7的にはアルゴリズムと呼んでいる。
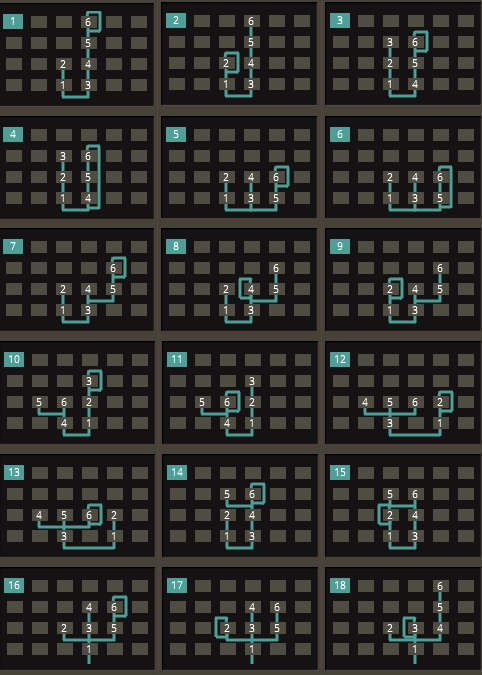

出力(一番下段)にあるオシレータをキャリアと呼び、それ以外をモジュレータと呼ぶ。アルゴリズムに応じて出力数は1~6個あり、複数の場合は、ミックスされて出力されることになる。
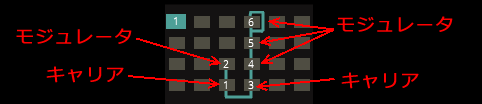
FM音源として、もっとも単純なかたちは、1個のキャリアと、1個のモジュレータの組み合わせ。 まずは、キャリア1個とモジュレータ1個の組み合わせを使って基本的な波形を作成してみる。 使えるアルゴリズムはいくつかあるが、5番を使用。オシレータは1と2を使用する。 FM音源を簡単な式にすると、まずサイン波の式を以下としてみる。a1は振幅で、f1は周波数とする。FM音源的には比率。
a1*sin(x*f1)
FM音源は、2つのサイン波を使って、次のようにして作り出す。括弧の中にもうひとつサイン波(モジュレータ)の式が入っている。
a1*sin(x*f1 + a2*sin(x*f2))
下は数理処理ソフトで描いたサイン波とFMによる矩形波。
sin(x + sin(x*2))
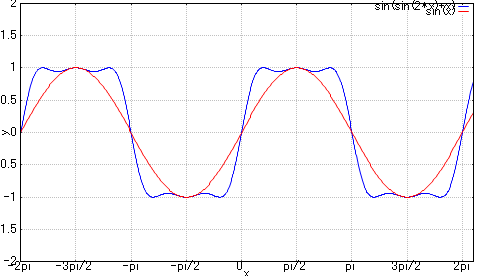
ちなみにラジオのFMの場合は、キャリアが放送局の周波数で、モジュレータが音声信号に相当する。
矩形波(くけいは) 奇数倍音
まず上記の矩形波をDEXEDで作ってみる。 矩形波は、理論的には奇数倍音を重ねていくとできる波形。振幅は倍音と同じ数で割って、小さくしていく。キャリアモジュレータ比率を1:2にすると奇数倍音だけを含む波形を作れる。ただ下記の通りキレイな矩形波ではない。数学的な波形とも若干異なる。
キャリア:モジュレータ比 = 1(level99):2(level69)
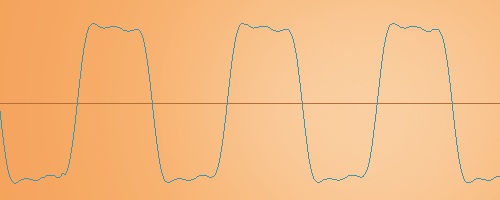
のこぎり波 整数倍音
のこぎり波は整数倍のサイン波を合成する。振幅は倍音と同じ数で割って、小さくしていくところがポイントだが、オシレータ2個では、満足いくのこりぎ波は作れない。
キャリア:モジュレータ比 = 1(level99):1(level64)
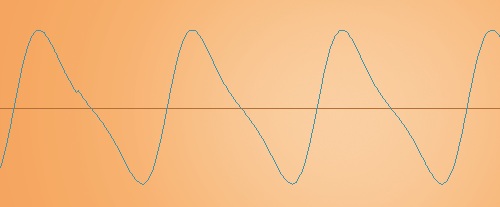
他の方法としては、オシレータ1個使ってフィードバックでも作れる。こちらの方がより鋭いエッジを作れるようだ。今回やってみて、キャリアのレベルによって、かかり具合が変わる事が判明。最大の99にしてしまうと、倍音が出すぎてしまう。
キャリアlevel97、FB = 7
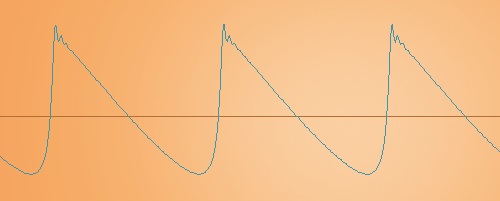
比率を変えてみる
キャリアcoarse1に対して、モジュレータcoarse0.5~31に変化させてみる。モジュレーターのレベルによって出音がかなり違うので録音してみた。サンプル音はA440Hz。
level99
level90
level80
level60
モジュレータのレベルが高いとランダムな倍音がプラスされているのがわかる。またモジュレーターの出力レベルを上げても倍音が増えていく。 ただ同じ傾向で変化しているわけではない。 その原因はデジタル処理ならではの折り返しノイズが入っているためで、直感的な音作りを妨げる要因となっている。 そのためFM音源の音作りは難しいと言われている。
まだ1個のモジュレーターならよいが、これが直列に数個重なったりすると、さらに傾向がつかみにくくなる。 それでも各倍音と基音との関係を知っているとかなり助けにはなる。当然のことだが、倍音は基音の倍数なので、高次倍音になるほど、音の飛びは少なくなる。 またモジュレータを整数にした場合は、作り出される音も通常の整数倍の倍音が中心となる。
下表は倍音の周波数だが、そのままcoarse(1~31)といる。
| 倍音 | 音程 | 音高差 | 音名 | 平均律よりの差 |
| 第1倍音 | ユニゾン | 0 | C3 | ±0 |
| 第2倍音 | 1オクターヴ | 12半音 | C4 | ±0 |
| 第3倍音 | 1オクターヴと完全5度 | 19.019550半音 | G4 | +1.955セント |
| 第4倍音 | 2オクターヴ | 24半音 | C5 | ±0 |
| 第5倍音 | 2オクターヴと長3度 | 27.863014半音 | E5 | -13.686セント |
| 第6倍音 | 2オクターヴと完全5度 | 31.019550半音 | G5 | +1.955セント |
| 第7倍音 | 2オクターヴと短7度 | 33.688259半音 | B♭5 | -31.174セント |
| 第8倍音 | 3オクターヴ | 36半音 | C6 | ±0 |
| 第9倍音 | 3オクターヴと長2度 | 38.039100半音 | D6 | +3.910セント |
| 第10倍音 | 3オクターヴと長3度 | 39.863014半音 | E6 | -13.686セント |
| 第11倍音 | 3オクターヴと増4度 | 41.513179半音 | F6-F♯6中間 | F#より-48.682セント |
| 第12倍音 | 3オクターヴと完全5度 | 43.019550半音 | G6 | +1.955セント |
| 第13倍音 | 3オクターヴと長6度 | 44.405277半音 | A6 | -59.472セント |
| 第14倍音 | 3オクターヴと短7度 | 45.688259半音 | B♭6 | -31.174セント |
| 第15倍音 | 3オクターヴと長7度 | 46.882687半音 | B6 | -11.731セント |
| 第16倍音 | 4オクターヴ | 48半音 | C7 | ±0 |
| 第17倍音 | 4オクターヴと半音 | C#7 | +5セント | |
| 第18倍音 | 4オクターヴと1音 | D7 | ||
| 第19倍音 | 4オクターヴと短3度 | Eb7 | ||
| 第20倍音 | 4オクターヴと長3度 | E7 | ||
| 第21倍音 | 4オクターヴと長3度+1/4音 | E7-F7中間 | ||
| 第22倍音 | 4オクターヴと長4度 | F7-F♯7中間 | ||
| 第23倍音 | 4オクターヴと増4度 | F#7 | ||
| 第24倍音 | 4オクターヴと完全5度 | G7 | ||
| 第25倍音 | 4オクターヴと増5度 | G#7 | ||
| 第26倍音 | 4オクターヴと長6度 | A7 | ||
| 第27倍音 | 4オクターヴと長6度+1/4音 | A7-A#7中間 | ||
| 第28倍音 | 4オクターヴと短7度 | A#7 | ||
| 第29倍音 | 4オクターヴと短7度+1/4音 | A#7-B7中間 | ||
| 第30倍音 | 4オクターヴと長7度 | B7 | ||
| 第31倍音 | 4オクターヴと長7度+1/4音 | B7-C8中間 |
上記を鍵盤で示すと下記のようになる。20倍音以降は半音よりも狭くなってしまうので、鍵盤では表し切れていない。

楽器の倍音構成
楽器の音が違って聞えるのは、倍音構成によるところが大きい。 FM音源では上記の操作で倍音構成が変化するので、実際の楽器の倍音構成に近いセッティングができれば、 再現できるのだが、FM音源の特性上、理論的に欲しい倍音を導き出すのは難しい。 一番単純な方法は、アルゴリズム32を使って、6個のオシレータを使って倍音を足していけば、それっぽくなる。 たとえば単純な倍音構成のオルガン(コルネット)は、基音 + (1オクターブ) + (1オクターヴと完全5度) + (2オクターヴ) + (2オクターヴと長3度)といった構成音になっている。これは1~5倍音で構成された音。 これをやってみると、オルガンぽい音にはなる。
この方法はFM音源の原理ではなく加算合成方式。倍音に当たる周波数のサイン波をミックスしただけにすぎない。実際の楽器の音を再現しようとすると、オシレーターの数がかなり必要となり不経済。 その点、FM音源は数個のオシレータで、いろいろなバリエーションの音を作れるので経済的といえる。ただ上記と同じ音を2オシレーターで作るのはやはり無理があるというもの。
モジュレータのレベルと倍音構成
モジュレータのレベルで、加味される倍音が違うので、どうなるかFFTで表示させてみた。
キャリア比1(level99):モジュレータ比1(level40)
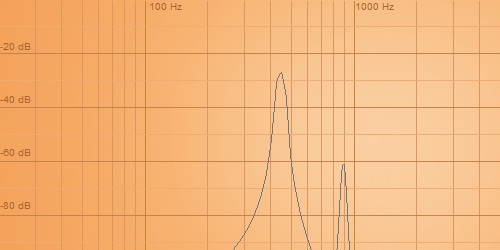
キャリア1(level99):モジュレータ1(level60)
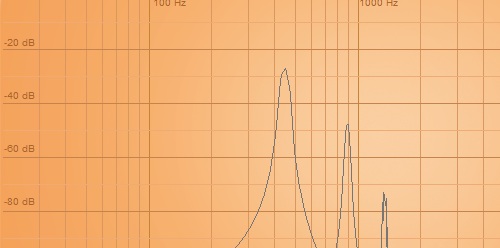
キャリア1(level99):モジュレータ1(level80)
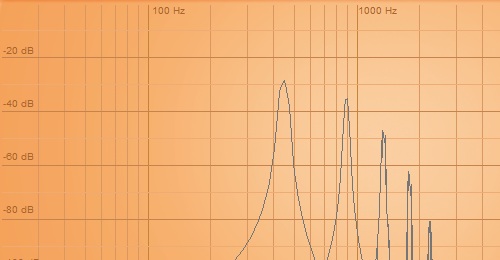
キャリア1(level99):モジュレータ1(level90)
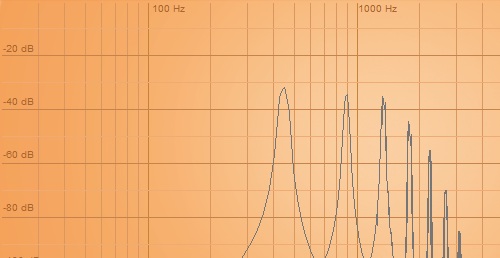
キャリア1(level99):モジュレータ1(level99)
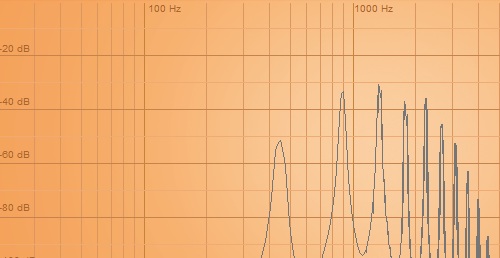
ここで判ることは、倍音は整数倍であること。そしてモジュレータレベルが低いと倍音が少ないということ。上げて行くと、倍音が増えていくが、倍音構成そのものは変わらないようだ。99まで上げて行くと、基音よりも倍音のレベルが高くなる。逆にモジュレータが最大レベルのときに最も音色的な特徴が出るので、ここで方向を決めてから、必要に応じてレベルを下げる方向で調整すれば、目的の音に到達しやすいかも。
FM音源はエイリアスノイズを積極的に使って音作りをしている。これが予測不可能な音の原因になっている。エイリアスノイズとは、デジタル処理で、ナイキスト周波数を超えると、折り返して低い可聴域にノイズが入ること。このノイズは普通の音として聞こえてしまうので質が悪い。アナログシンセをデジタルで再現する場合、もっとも注意すべき点の一つだが、FM音源は逆にエイリアスノイズを活用しているので、対策をとるわけにもいかず、こうなってしまったと言える。デジタル的には何の対策もしていないので、とてもシンプルでピュアとも言える。
折り返しが入った場合、ドレミを低い方から順次鳴らすと、本来きれいに上がっていくはずが、下サンプルのように途中でおかしな音程が出始める。これが折り返して可聴域に入った音で、FM音源を扱う場合気を付ける必要がある。下サンプルはモジュレータを2倍音にしてレベル99にしている。
下アニメはキャリアに対してモジュレータの比を上げていった場合のスペクトラムになる。折り返すイメージが分かると思う。最高音まで行ったら戻ってきて、最低音まで行ったら、また戻るという具合だ。これを音でイメージするのは至難の業である。 使う音程にも依存するが、折り返しが発生しない範囲で使う場合は、破綻が起きにくい。また折り返しが発生するような条件でもレベルを下げることにより、明らかな破綻は避けて使うことが可能。
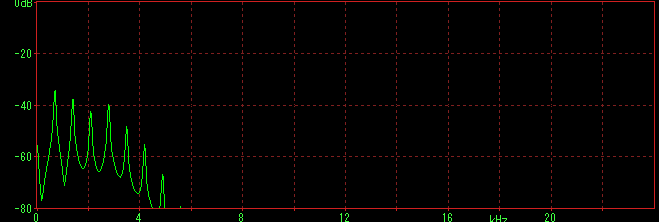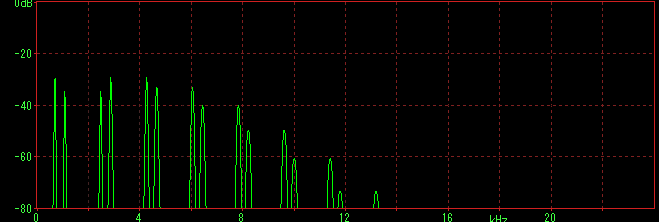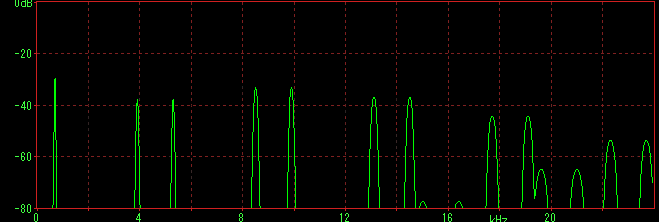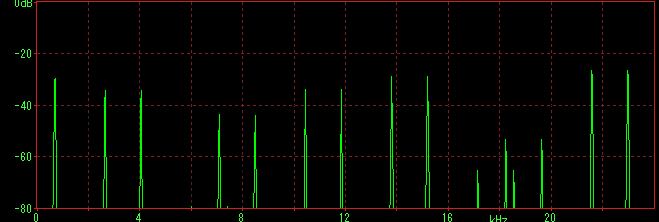
実際の音作り
音程のある楽器の倍音構成は、基本的に整数倍の倍音を中心に作られている。まずこれがないと、ちゃんとした音程感を得にくいので、これをしっかり作ることが重要。整数倍を扱える組み合わせは、矩形波やのこぎり波や、サイン波そのものなどに限られるので、そこで骨格を作る。
そして楽器の音の多くはアタックに特徴があるので、そこに金属的な響きを与えたり、ノイズっぽくしたり、様々なアタック音を加える。これだけでそれっぽい音が作れるし、実際のヤマハのプリセットも伸びる音程感のある音と、アタック音で構成されている。アナログシンセでは、このアタックを自在に作れなかったため、FM音源が重宝された。
FM音源が苦手なところは、きれいなエッジのあるのこぎり波が作りにくいところだろうか。どこか丸い感じで木管的になりやすいし、無理すると金属的になってしまう。柔らかいストリングス系の音はアナログシンセにはかなわない。
波形で動的に見てみる
JavaScriptでキャリアとモジュレータの関係を波形で表示するプログラムを組んでみた。音で聴くと複雑だが、このように波形を動かしながら見ると、どのように変化していくのか直感的で分かりやすい。 とりあえずDEXEDの表示と数値を合わせておいた。 最大レベルを近づけてみた。途中の値は、結構違うので注意。 DEXEDは、もっと緩やかにレベルが上がっていき、最後の方で一気に上昇する。
スライダーでいじれるのはキャリア(青)、モジュレータ1(赤)、モジュレータ2(オレンジ)、モジュレータ3(紫)のcoarse(周波数比)とLevelになる。これは接続順でもある。そして緑の波形がキャリアからの出力波形となる。

またモジュレータは上記のように3つ直列してあり、DEXED(DX7)の最大(アルゴリズム1、2)の状態。モジュレータを少なくしたい場合はLevelを0にすれば無効となる。値の範囲はDEXEDと同じにしてみた。
これをしばらくいじっていればDEXEDで音作りする際、迷うことは少なくなると思う。 たとえば、理想に近いのこぎり波や矩形波を作ろうと思うと、モジュレータは多いほどいい。DEXEDではモジュレータ3つが最大なので、その範囲で作るしかない。 上記でシミュレーションすれば、簡単にのこぎり波、矩形波の値を導き出せる。 ただDEXEDの数値とは一致しない。最大レベルで調整してあるので、途中のレベルの場合は調整が必要。 (その後、dexedのソースをチラ見したら、曲線ではなく、ステップ上の数値になっているぽいので、再現するにはステップごとの数値を見極めないと無理っぽい。)
