32-bit float IEEE 754 浮動小数点数について
32-bit floatについて改めて調べてみた。少し疑問もあったので、それを明確にするのが目的。はじめネット上の情報で理解できるかと高を括っていたが、知りたいことがズバリ書いているところが見つからなかった。仕方なく32-bit float IEEE 754の原理を調べて、その後はプログラムを組んで確認していった。そのときのメモ。
無圧縮音声ファイルのWAV 32-bit floatを扱うための知識
floatの数値で音声ファイルに重要なのは、-1~0~+1の範囲。下の絵はAudacityのトラック部分。上下のレベルは-1~0~+1に対応している。この部分が、どのような精度で記録されていくのかを調べてみた。16bitや24bitと比較してどうなのか? という点も重要。その差は問題となるのか? など。 WAVフォーマットでは32-bit floatをそのまま利用しているので、1を超える数値や-1以下の数値も扱えてしまう。そういう部分にも触れたいと思う。
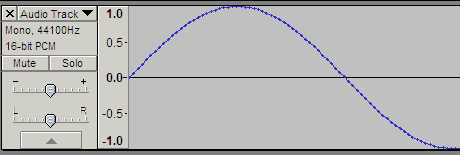
疑問点
そもそもの解像度を知りたいというところから始まった。漠然とかなりの解像度であることは分かっていたが、計算すると、かなり不思議な値が出てきた。0に近いほど精度が上がっていたり・・・ やたら大きな数も扱えたり・・・ 表現出来る範囲は32bitのはずだが・・・ こんな感じで、その仕組みを知る必要性を感じはじめた。
ビットとは?
デジタル音声ファイルで、よく聞くビットというのは、Audio bit depth のことで、音量レベルの解像度のこと。CDでは16bitが使われている。最近のデジタルレコーダーなどは24bitなどが採用されている。波形編集ソフトのAudacityでは様々なビットを扱うことができる。このビット数が高いほど細かな音量差を表現出来ると考えてよい。ただこのページの32-bit floatは、ビットの後にfloatという言葉が付いている。floatは浮動小数点数が扱えることを意味する。ビット数は同じでも表現出来る数値が違ってくる。
浮動小数点数
Javaで扱える数字の型はいくつかある。その中でfloat、doubleは小数を直接扱うことができる。つまりこれ以外は少数は直接扱えない整数型。floatは浮動小数点型といわれる型。doubleはビット数を上げて精度をより高めたもの。ここでは基本となるfloatのみ扱うことにする。
音声ファイルと各ビット数の解像度
音響機器では0dBというのが最大音量と決められている。パソコンでは、この0dBを+1もしくは-1として扱うことにして、無音を0としている。下はAudacityのゲインをdB表示させたところ。音声は基本的に0dB以下で構成される。
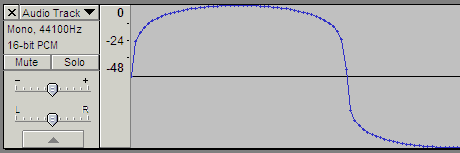
16bitの場合、表現出来る整数は0~2^16(65536通り)。ただ、音声ファイルはプラスマイナスが表現できないと困るので、2の補数を使うことで、それを実現している。Javaで扱えるshortの整数型そのもので、-32768~+32767 を扱うことができる。-32768(32768 0x8000) が -1 に相当し、+32767(32767 0x7FFF) が +0.9999(約1)に相当する。音の解像度は 65536 段階となる。
24bitで表現出来る整数は0~2^24(16777216通り)で、16bitと同じように2の補数を使ってプラスマイナスを表現し、-8388608~+8388607 が利用されている。解像度は16bitの256倍もある。つまり、16ビットの階段ひとつ分に256段の階段をつけるようなもの。かなり細かな音量差を表現できるのが分かる。
32bitはどうか? これはfloatではないもの。0~2^32(4294967296通り)。16bitと同じように2の補数を使ってプラスマイナスを表現すると -2147483648~ +2147483647 となる。解像度は高く24bitの256倍。16bitの65536倍となる。ただ現在のところ高負荷のため32bitは主流ではない。Audacityでは32bitで書き出すことは可能。
32bit floatはどうか? これは単純に比較できない。整数を扱わないので、その構造から理解する必要がある。
32bit floatの構造
32bitなので、2進数の32桁ということに変わりはない。例えばこんな感じ。
0011 1111 1000 0000 0000 0000 0000 0000
0と1の組合せで32桁。とても読みにくい。これを16進数で表現すると、4桁分を一文字で表現できるようになるので人間でも読みやすくなる。
3F80 0000
こんな感じ。プログラムでは16進数という意味を込めて0xを頭につける。
0x3F80 0000
単なる32bitであれば、2進数を変換して10進数にして、必要に応じて2の補数を使ってプラスマイナスに分けるのだが、floatではやや複雑な手続きをする。まず下のように3つの部位に分かれる。
符号部(sign 1bit)、 指数部(exponent 8bit)、仮数(かすう)部(mantissa 23bit)
0011 1111 1000 0000 0000 0000 0000 0000
次にこれらを、下のルールに則って値を求める。
float = (-1)^(符号部) × 2^(指数部-127) × 1.仮数部
上記に入れることでfloatの値を導く仕掛け。符号部と指数部は10進数で計算。指数部は2進数のままにして、最後に10進数なりに変換するというイメージ。
例1:
0x3F80 0000
2進数表記では
0011 1111 1000 0000 0000 0000 0000 0000
こうなるので、
符号部は0。
指数部は0111 1111 となり、10進数では127となる。
仮数部は000 0000 0000 0000 0000 0000となる。
float = (-1)^(0) × 2^(127-127) × 1.000 0000 0000 0000 0000 0000
= 1 x 1 x 1.0
= 1.0
となり、10進数の1.0を表現している。
例2:
3f000000
2進数表記では
0011 1111 0000 0000 0000 0000 0000 0000
符号部は0。
指数部は0111 1110 となり、10進数では126となる。
仮数部は000 0000 0000 0000 0000 0000となる。
float = (-1)^(0) × 2^(126-127) × 1.000 0000 0000 0000 0000 0000
= 1 x 0.5 x 1.0
= 0.5
となり、10進数の0.5を表現している。
例3:
仮数部が1以外になるような例
40400000
2進数表記では
0100 0000 0100 0000 0000 0000 0000 0000
符号部は0。
指数部は1000 0000 となり、10進数では128となる。
仮数部は100 0000 0000 0000 0000 0000となる。
float = (-1)^(0) × 2^(128-127) × 1.100 0000 0000 0000 0000 0000
= 1 x 2 x 1.1
指数を2進数にかけると桁がズレる。この場合は1桁上がる。ビットシフトのようなもの。
= 11
10進数変換
= 3.0
10進数の3.0となる。
こんな感じで計算していくのだが、例外とかいろいろある。
floatが表現出来る数値範囲
Javaの本には、こんな感じで載っていた。
プラスマイナス 1.40239846e-45(非正規化数) ~ 3.40282347e+38
自分でJavaでやってみると以下の範囲になる。
プラスマイナス 1.401298e-45(非正規化数) ~ 3.40282347e+38
これでピンと来る人は、かなり数値に慣れている人。普通の感覚的に直すと。
プラスマイナス
0.000000000000000000000000000000000000000000001401298464324817
~
340,282,346,638,528,860,000,000,000,000,000,000,000.0
の範囲で数値化できる。こんな書き方すると0がいくつあるのか分からなくなるので本当はしない。
これに加えて、当然 0 も表現できるし、なんと無限大も表現できる。
いくつかの代表的な数値をそれぞれの進数で表記してみると以下のようになる。
Decが10進数、 Hexが16進数、 Binが2進数。
Dec 0.0
Hex 00000000
Bin 00000000000000000000000000000000
Dec -0.0
Hex 80000000
Bin 10000000000000000000000000000000
Dec 1.0
Hex 3f800000
Bin 00111111100000000000000000000000
Dec -1.0
Hex bf800000
Bin 10111111100000000000000000000000
最大(無限大)
Dec ∞ Infinity
Hex 7f800000
Bin 01111111100000000000000000000000
最大値
Dec 3.4028235e+38
Hex 7f7fffff
Bin 01111111011111111111111111111111
最小値(正規化数)
Dec 1.17549435e-38
Hex 00800000
Bin 00000000100000000000000000000000
最小値(非正規化数)
Dec 1.401298e-45
Hex 00000001
Bin 00000000000000000000000000000001
非数 NaN(Not a Number)
Dec NaN
Hex 7F800001~7FFFFFFF
Bin 01111111100000000000000000000001 ~
01111111111111111111111111111111
floatの解像度
そもそもの疑問はここだった。32bitという有限の2進数が表現できる組合わせは、4294967296通りであり、約43億弱ということになる。この解像度で無限大まで表現したら、各段はものすごく大きくなってしまう。では、どういう仕組みになっているのか?
結論から言うと0に近い数ほど解像度が高く、数値が大きくなるたびに1段あたりが大きくなっていく。。floatでは有効桁は6~7桁までで、それ以下は適当に丸められるので、すごく大きな数と、小さな数の計算は意味がなくなってしまう。
例えば10進数で、
99999999999999999999999999999999999999.0
という数字をfloatで表示させるだけで、
99,999,996,802,856,920,000,000,000,000,000,000,000.0
こんな感じになってしまう。上から7桁目までは、正確だけど、それ以降はあれれ?という結果になっている。内部的な構造を観察すると、表現出来る桁数に限界があるのが分かると思う。その桁数を指数を使ってスライドしているだけに過ぎない。10進数で7桁より下は表示されていても、参考にすらしないほうがよい。大きな数では、1の位とか10の位とかなじみのある桁が全然ダメになるのに対して、1以下の小数は都合よくまとまってくれる。
例えばこんな数値の場合
0.000000000000000123456789123456789
floatでは
0.000000000000000123456785832878190
こうなる。やはり9という数字辺りからおかしくなるが、これは切り捨てても普通は問題にならない。
次にfloatで表現出来る0よりも大きくて一番小さい数値(非正規化数)は前述の通り、
1.401298e-45
であり、
0.00000000000000000000000000000000000000000000140129846432481700000
という数値。
これよりもひとつ大きい数値は?
0.00000000000000000000000000000000000000000000280259692864963400000
こうなる。10進数で表現するよりも16進数や2進数の方が実は分かりやすい。
16進数だと次のようになる。
0x00000001
0x00000002
・・・・・
なんてことはない。一番下の数値がひとつ増えただけ。
でも10進数を見ると2倍になっている。
さらに10進数で小さい順に並べていくとこうなる。
1.401298e-45
2.802597e-45
4.203895e-45
5.605194e-45
7.006492e-45
8.407791e-45
9.809089e-45
1.121039e-44
1.261169e-44
1.401298e-44
1.541428e-44
1.681558e-44
1.821688e-44
1.961818e-44
・・・・・
つまり最小の1.401298e-45の倍数になっている。
次に正規化数の最小16進数では以下のようになる。
0x00800000
0x00800001
0x00800002
・・・・・
10進数で表示させると以下のようになる。この段階も1.401298e-45の倍数。有効桁ギリギリが変化しているのが分かる。
1.17549435E-38
1.1754945E-38
1.1754946E-38
1.1754948E-38
1.1754949E-38
1.175495E-38
・・・・・
次に、指数が上がった16進数は
0x01000000
0x01000001
0x01000002
・・・・・
10進数では
4.70197740328915e-38
4.701977963808536e-38
4.701978524327921e-38
・・・・・
差は 2.80259693e-45 で、先の指数に対して2倍の大きさになっている。
次に、指数が上がった16進数は
0x01800000
0x01800001
0x01800002
・・・・・
10進数では
4.70197740328915e-38
4.701977963808536e-38
4.701978524327921e-38
・・・・・
差は5.6051938e-45。さらに2倍の大きさになっている。はじめの4倍。
指数がひとつ上がると、2倍の大きさの階段に拡大していくのが分かる。
解像度としては仮数部の組合せが23bit+暗黙の1があるけど、下のように計算してみた。
2^23=8388608 通り
これに指数をかけるが、ここでは0~1までに限定すると、-1~-127で127通りがある。これに1を合わせるので+1が必要。
8388608 * 127 + 1 = 1065353217
となる。サウンドで使える0~1.0の解像度は約10.65億通りという計算になる。プラスマイナスを合わせれば約2倍となる。
ただ、0周辺はダイナミックレンジに応じて完全に埋もれてしまうので、実質使える部分はもっと少ない。例えば16bitの96dBで計算すると、10億にまで減る。あまり減ったという感覚はないけど、0.65億は完全に埋もれているわけだ。
下図はプログラムを組んで、0~1.0までの点を打ってみた。点は指数部がひとつ上がるたびに打っているので128点ある。各点の間には等間隔に仮数部の8388608点が存在している。0付近は無数に点があるのに、途中から急激に1.0に向かっている。0.5から1.0直前までは指数の桁は変わらない。
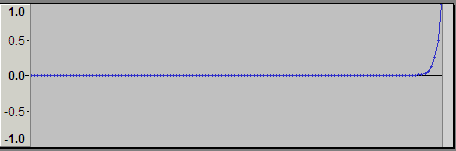
下図は急激に上がっている部分の拡大。上段がリニア表示で、下段がdB表示。dB表示するとほぼ直線状になることが分かる。Audacityでは最大で-145dBから0dBの表示なので、途中から斜めに伸びているが、理想的な表示であれば、完全に斜めの直線状に点が並ぶはず。人間の耳は対数的な感覚を持っているので、floatの解像度の変化はあっているかもしれない。ちなみに-145dB以下は人の聴ける範囲を完全に超えている小ささなので、通常は無視してよい範囲。
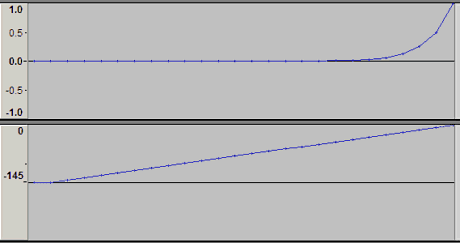
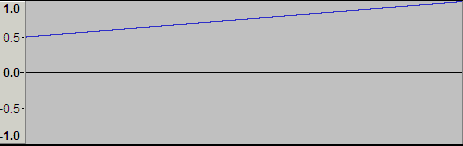
下図は0.5~1.0の8388609点。44100Hzで各点を打ったので、約3分のデータになっている。リニア表示で直線になる。各点のステップは等間隔。その間隔は10進数で 0.0000000596046448 となる。
32bitと32bit floatの比較
まずは最小値の比較
32bit:
0.0000000004656612873077392578125
32bit flaot: 非正規化数
0.000000000000000000000000000000000000000000001401298464324817
32bit flaot: 正規化数
0.000000000000000000000000000000000000011754943508222875
圧倒的に小さい数を表せるのが32bit float。
1.0とその次に小さい値の比較
32bit:
0.999999999534338712692260742188
1.0との差は
0.0000000004656612873077392578125
32bit flaot:
0.9999999403953552 (0x3f7fffff)
1.0との差は
0.0000000596046448
1.0に近いと32bitの方が解像度が高い。
32bitは常に 0.0000000004656612873077392578125 ステップで動作する。つまり等間隔。floatは0に近いほど解像度が上がるが、指数が同じ間は等間隔になる。サウンドの場合、特に0.5~1.0の間は指数ひとつ分の解像度しかない。つまり8388608点しかない。一方32bitは1073741824点であり、その差は128倍。32bit float(0.5~1)の解像度の低さが実感できるだろう。ちなみに24bitの0.5~1.0は4194304点。32bit floatはかろうじて、24bitの2倍の解像度がある。
32bit floatは0に近いと解像度が上がる。32bitと同等の解像度になれるのは、0.00390625以下のときで、dBで計算すると-54.1854dB以下のとき。レベルが下がると劇的に解像度は上がっていくのだが、サウンドにおいては、90dB以下のノイズに埋もれている部分は解像度が高くても、あまり意味のない話になってしまう。
ということで実用的な範囲での解像度では32bitが上だが、Audacityでは現在のバージョンでは32bitをサポートしていない(読み込み、書き出しは可)。またVSTなども32bit floatか64bit doubleで計算を行う仕様になっている。計算においては何かと小数点を扱えた方が都合がよく、整数型の32bitは今後も使われそうもない。
サウンド加工した場合、16、24bitに比べ32bit floatのよい点は?
まず、サウンドの加工をする場合、VSTなどを見ても内部的にはfloat、doubleを使って計算している。そして加工後に各ビット深度にマッピングすることになる。そのときの誤差が問題になったりする。16bitや24bitはどうしても誤差が出てしまい避けることはできない。繰り返し加工をすると、僅かな誤差も拡大し、大きな問題になってくる。一方32bit-floatは計算結果を変換せず、そのままアウトプットできる。マッピングによる誤差がないだけでなく、変換ロスがないため実は高速に処理できる。ということで加工中は32bit-floatにしておくべきだと思う。最後の最後に1回だけ16bitなど汎用bitに落とすという使い方が正解だと思う。
あとは小音量時の分解能が32bit-floatは圧倒的なので、やはり差があるように思う。例えばリバーブなどを薄くかけると、その残響成分などは質が違って聴こえる。16bitと比較すると話にならないぐらいの差が出てしまう。
