dB(デシベル)とbit(ビット)の関係について
デシベルって?
サウンドでよく使われるデシベルは、基準となる音に対しての対数比で音量差を表したもの。 なぜdBを使うかというと、いくつかの理由がある。 小さな数から大きな数までを一緒に扱いやすく、それらを簡単に計算することができるから。 また対数は人の感覚に近く、イメージしやすいことなどが上げられる。
人の聴覚は小さい音に敏感に反応し、大音量になるほど鈍感になっていくるというもの。これがdBであらわされた数値に近い。例えば物理量で10倍の音量になっても、そこまで大きくなったとは感じない。2倍程度に感じるというのが一般的な話。 デシベル表示だと20dBということになるが、 ベル表示では一桁減らして2となり、ちょうど人間の感覚に近い数値になる。 また人は0~120dB(100万倍)までが聞き取れる範囲。このことはオーディオ等に求められているダイナミックレンジは120dBあれば十分ということを意味する。 オーディオ機器などでは最大音量を基準とし、0dBと決めている。そのため扱われる音量はマイナスdBで表示される。
物理量からdB(電圧比)を導く計算式
G[dB] = 20log10(Vo/Vi)
G:デシベル換算した比
Vi:入力音量
Vo:出力音量
反対にdB(電圧比)から物理量を導く計算式
Vo/Vi = 10^(G/20)
| 物理量 | デシベル |
| 等倍 | 0dB |
| 1/2 | -6dB |
| 1/3 | -10dB |
| 1/10 | -20dB |
| 1/100 | -40dB |
| 1/1000 | -60dB |
| 1/1万 | -80dB |
| 1/10万 | -100dB |
| 1/100万 | -120dB |
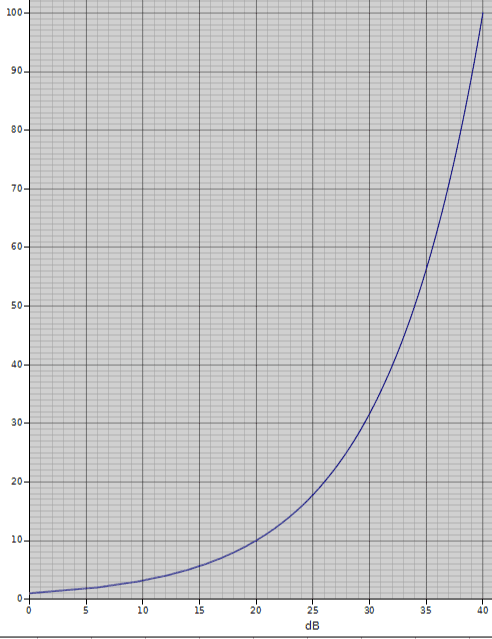
下記はデシベルと物理量のグラフ。上記と違いプラスで表記している。見やすく実用的な範囲の40dBまでをグラフにしてみた。 約30dBまでは、物理量がデシベル値よりも小さく、その後は逆転し、デシベル値がそれほど増えなくても、物理量は、すさまじい勢いで大きくなっていく。 感覚的にあると便利なのは20dB差は10倍だということ。40dB差であれば100倍で、60dB差であれば1000倍という感じ。
ビットって?
サウンドのビットは音量の分解能をあらわす。画像と同じように、解像度(Resolution)、ビット深度、量子化ビット数など、様々な言われ方もする。オーディオ用に使われている最もポピュラーなビット数は16bit。最近では24bitも使われるようになった。サウンド編集では32bit-floatなども使われている。Audacityでは、これらを切り替えて編集できるようになっている。それぞれの解像度は以下のようになる。(32bit-floatは扱いが違うので除外)下の数値を-1.0~+1.0 にマッピングして使用している。
16dB:2^16 = 65536
24dB:2^24 = 16777216
32dB:2^32 = 4294967296
デシベルとビットの関係
ビット数によって、記録できる最小音量から最大音量までの比率が違ってくる。これをダイナミックレンジと言う。ここでデシベルを使うことで分かりやすく表現することができる。一般的に各ビットのダイナミックレンジは以下のように言われている。
16bitは約96dB
24bitは約144dB
32bitは約192dB
各ビットで最小音量から最大音量の範囲が決まってしまうので、範囲外の大音量や小音量は記録できなくなる。普通、最大音量がつぶれるのは嫌なので、最大音量が入るように録音する。そうすると生では聞こえる小さい音は、録音後聞き取れなくなるが、問題になることはまずない。ポピュラーミュージックでは聴きやすくするため音量差は圧縮調整されているぐらい。また16bit以上では最小音量付近は機器のノイズに埋もれる場合がほとんど。24bitになると、人の聞き取れる範囲を超えているので、ダイナミックレンジには余裕がある。32bitはオーバースペックに思えるかもしれないが、メリットはダイナミックレンジだけではないので利用価値は十分ある。
どのようにしてビットのデシベルを求めるのか
下に説明用として3bitの例を示す。3bitは2進数が3桁ということだから、 2^3 の8通りのパターンが存在する。10進数と2進数で書くと、
0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111
こうなる。これを2の補数を使ってプラスマイナスに振り分ける。すると10進数では次のような意味になる
0 = 000
1 = 001
2 = 010
3 = 011
-4 = 100
-3 = 101
-2 = 110
-1 = 111
このような関係にしてしまえばプラスマイナスの足し算が簡単にできる。実際使われている16bit、24bitも同じ考え方。3bitの場合はマイナス-4~3の間となる。マイナスの方がひとつ多い。これをサウンドでは-1~1にマッピングして使うことになる。3bitの場合、数が少なすぎて1から離れた0.75がプラスの最大音量となってしまうが、このまま説明したい。
0 = 000 = 0
1 = 001 = 0.25
2 = 010 = 0.5
3 = 011 = 0.75
-4 = 100 = -1
-3 = 101 = -0.75
-2 = 110 = -0.5
-1 = 111 = -0.25
下に3bitの最大音量と最小音量を示してみた。ダイナミックレンジを考えるときに重要なのは最大音量はマイナスの最小からプラスの最大までを言う。スピーカーの動きから連想すると、一番引っ込んだ状態から一気に一番出っ張った状態までの動きが最大の幅となる。3bitの場合は7段ということになる。それに対して最小は1段分をカウントする。つまり1。スピーカーの動きとしては負荷のない状態から、ちょこっと前に出てきたようなもの。マイナスへ行く必要もない。動きがあればそれは音になる。これを比であらわすと、 7:1 となる。最小音量から見れば、その7倍の音量まで扱うことが可能。
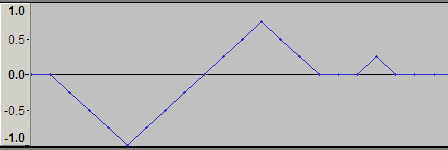
これをdBで計算すると、7倍の音量差ということは、
20log (7/1) = 16.9019608dB
となる。これが3bitで扱えるダイナミックレンジとなる。ちなみに1段から2段の差は2倍なので、
20log (2/1) = 6.0205999dB
となる。よくこの数値を使って単純にビット数に掛ければダイナミックレンジが計算できるような紹介がある。3bitを計算してみると、
3bit * 6.0206dB = 18.0617997dB
となって大きくなってしまう。3bitの場合、その誤差は大きすぎて問題だが、16bitもあると問題ない。実際に計算してみると、まず本来の計算ではこうなる。
16bit : 20log ((2^16)-1) = 96.3294661 dB
24bit : 20log ((2^24)-1) = 144.4943974 dB
32bit : 20log ((2^32)-1) = 192.6591972 dB
簡易計算では、
16bit : 16bit *
6.0206dB = 96.3295986 dB
24bit : 24bit *
6.0206dB = 144.4943979 dB
32bit : 32bit *
6.0206dB = 192.6591972 dB
ビットが大きくなるほど誤差が少なくなっているのが分かると思う。
ビットの使い分け
長いこと16bitが主流であったが、最近は、録音装置、再生装置、及びソフト共に24bitが利用可能になってきている。ただCDなどは16bit規格で普及してしまっているから、簡単には24bitへの移行は出来ないだろうし、完成された音は16bitでも不満はない。ビットは大きいほど高解像度であるので、品質の面ではよいのだが、録音から再生まで、すべてにおいて高解像度にする必要性はない。むしろ、うまく使い分けるほうが経済的である。ビットの大きさ順に用途を並べると下のようになる。
編集加工 > 録音 > 再生(完成
最もビット深度が求められるのは編集加工のプロセス。このプロセスは音量を細かくいじりまくることが多く、計算の誤差が出やすい。可能な限り誤差を少なくするためにビット深度は深ければ深いほど品質を上げることが可能。ビットを上げることでデータ量と計算量は増大するが、それだけのメリットはある。
録音はビット深度よりも、マイクやマイクプリアンプなどの機材の性能が大きい。これらの機材の性能が悪ければ、ノイズに埋もれてビット深度を生かしきれない。ただ、ノイズだけの話でもないので、ビット深度の高いものが利用できるなら、それらを利用すべきだろう。
再生は、多くの場合最終的な作品ということになるので、利用したいシーンが自ずと決まってしまうだろう。最近は音質よりもデータを小さくしたいという要求が強く、圧縮音源がスタンダードになってしまった。再生という意味では過酷な条件にある。でも仕方なく利用形態にあわせたフォーマットにするしかない。
多くの場合は16bitになると思う。録音、編集過程で24bitを使っていても、最終的に16bitにしてしまっては意味がないのでは?と思うかもしれないが、実際にはそんなことはなく、品質は明らかに違うものになる。例えば、
A: 録音16bit - 編集加工16bit - 再生16bit
B: 録音24bit - 編集加工32bit - 再生16bit
上記は全く品質が違ってくる。当然作業内容に依存するが、うまく行えばBが圧倒的に繊細なはずだ。
最近の再生装置は16bitを補間している場合も多く、実際のデータよりも高品質に再生される。ビットということではないが、圧縮音源で欠けてしまったデータを復元させて再生するということも普通にされている。劣化してしまった最終音源も、あの手この手で救済されているようだ。
